Page 18 - โครงสร้างข้อมูลและขั้นตอนวิธี
P. 18
2-8 โครงสร้างข้อมูลและขั้นตอนวิธี
8 6x2 x2 + 4x + 1
6 x2
4
2
0
0.0 0.5 1.0 1.5 2.0 2.5 3.0
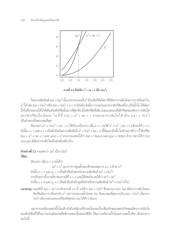
ภาพท ี่ 2.2 ฟงั กช์ นั x2 + 4x + 1 เป็น O(x2)
ในค วามส ัมพันธ์ f(x) = O(x2) น้ัน สามารถแ ทนที่ x2 ด้วยฟ ังก์ชันใดๆ ท่ีม ีอัตราก ารเติบโตม ากกว่าห รือเท่ากับ
x2 ได้ เช่น f(x) = O(x3) หรือ f(x) = O(x2 + x + 7) เป็นต้น ดังน ้ัน การจ ะป ระมาณว ่าฟังก์ชันหน่ึงๆ เป็นบ ิ๊กโอ ให้เลือก
บก๊ิ โอทป่ี ระมาณไดใ้ กลเ้ คยี งก บั ฟงั กช์ นั น น้ั มากทส่ี ดุ คอื เปน็ ฟงั กช์ นั ท อ่ี ธบิ ายข อบเขตบ นทเ่ี ลก็ ทส่ี ดุ ข องอ ตั ราก ารเตบิ โต
ของ ฟั ง ก์ชัน น้ั น น่ันเ อง ใ น ท่ี น้ี f ( x) = x2 + 4x + 1 ป ระมาณการ เติบโ ตไ ด้ เป็ น f( x ) = O( x2 )
เป็นค�ำต อบท่ีเหมาะสมท่ีสุด
สังเกตว่า x2 = O(x2 + 4x + 1) ได้ด้วย เนื่องจาก เม่ือ x > 1 จะได้ x2 < x2 + 4x + 1 แล้วจะได้ c = 1
ดังน ั้น c = 1 และ x = 1 เป็นต ัวยืนยันค วามส ัมพันธ์ x2 = O(x2 + 4x + 1) น้ีน ่ันเอง ดังน ั้น ในต ัวอย่างท ่ี 2.1 นี้ ฟังก์ชัน
f(x) = x2 + 4x + 1 และ g(x) = x2 สามารถแสดงได้ว่า f(x) = O(g(x)) และ g(x) = O(f(x)) ด้วย กล่าวได้ว่า f(x)
และ g(x) มีอ ัตราก ารเติบโตเป็นอ ันดับเดียวกัน
ตวั อยา่ งท่ี 2.2 จงแ สดงว ่า 3x2 เป็น O(x3)
วิธีท�ำ
สังเกตว ่า เมื่อ x > 3 จะได้ว่า
3x2 < x3 (มาจ ากก ารค ูณท ้ังสองข ้างของส มการ x > 3 ด้วย x2)
ดังน ั้น c = 1 และ x0 = 3 เป็นต ัวยืนยันส �ำหรับความสัมพันธ์ 3x2 = O(x3)
จากต ัวอย่างนี้ อาจพ ิจารณาก รณีท ่ี x > 1 แทนได้เช่นก ัน จะได้ว่า 3x2 < 3x3
ดังน ้ัน c = 3 และ x0 = 1 เป็นต ัวยืนยันอีกค ู่หนึ่งส �ำหรับความส ัมพันธ์ 3x2 = O(x3) ด้วย
หมายเหต:ุ ส มมติให้ f(x) = 3x2 จากต ัวอย่างที่ 2.2 นี้ จะได้ว่า f(x) = O(x3) ซึ่งหมายความว่า f(x) มีอ ัตราการเติบโตของ
ฟังก์ชันน ้อยก ว่าหรือเท่ากับ x3 แต่การประม าณบิ๊กโอข อง f(x) ที่เหมาะส มที่สุดค วรเป็น f(x) = O(x2) เนื่องจาก
O(x2) อธิบายข อบเขตบ นที่น ้อยที่สุดของ f(x) ได้ดีก ว่านั่นเอง
นอกจากบทนิยามของบ๊ิกโอแล้ว ยังมีบทนิยามที่น ่าสนใจและเกี่ยวข้องกับขอบเขตจ�ำกัดของอัตราการเติบโต
ของฟังก์ชันท่ีใช้ในการประเมินประสิทธิภาพของขั้นตอนวิธีอีก ได้แก่ บทนิยามบ๊ิกโอเมกาและบิ๊กทีตา ดังจะกล่าว
ต่อไปน้ี